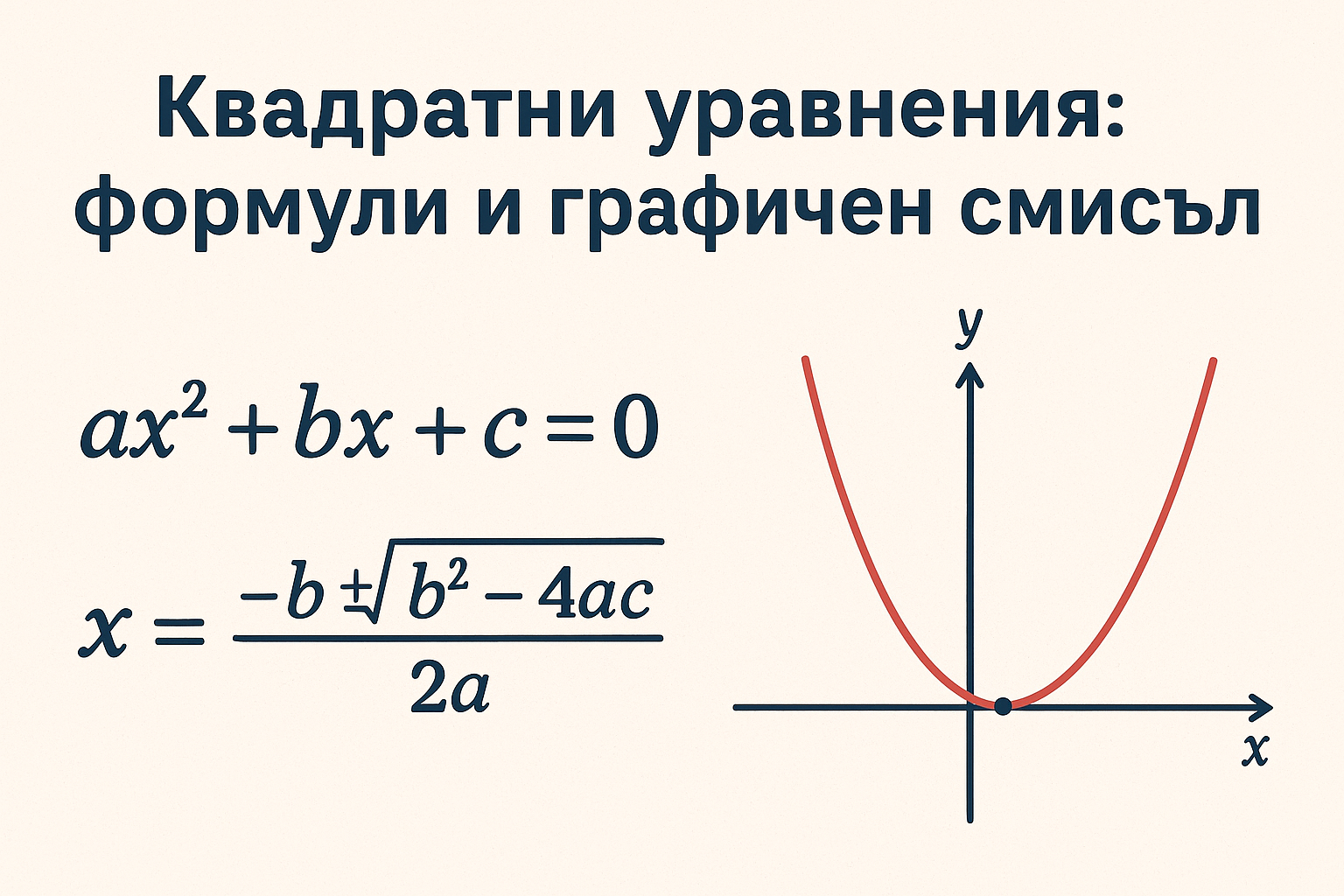
☰☰
Квадратни уравнения: формули и графичен смисъл

Квадратни уравнения: формули и графичен смисъл

Стефан Стратиев, Математика, 29 окт 2025

Въведение

Квадратните уравнения са сред най-важните теми в училищната математика. Те моделират движение на тела,
оптимизационни задачи, геометрични зависимости и още много практически ситуации. В тази статия ще съберем на
едно място формулите, методите и графичния смисъл, ще решим примери стъпка по стъпка и ще завършим с кратък тест
и домашни упражнения. Целта е ясна: когато видиш квадратно уравнение, да знаеш бърз и надежден план за действие.

Ключови формули и идеи

  • Общ вид: ax² + bx + c = 0, a ≠ 0

  • Дискриминанта: D = b² − 4ac

    • D > 0 → два различни реални корена

    • D = 0 → двоен реален корен

    • D < 0 → два комплексни корена

  • Формула за корените: x = [−b ± √D] / (2a)

  • Графика: y = ax² + bx + c е парабола

    • Върхът: x_v = −b/(2a), y_v = f(x_v)

    • Пресечки с Ox: решенията на уравнението

    • Посока на отваряне: a > 0 нагоре, a < 0 надолу

  • Нормализиране: когато е удобно, делим на a и търсим разлагане

Квадратното уравнение има най-много два реални корена. Ако те са реални, параболата пресича Ox в съответните
точки. При двоен корен върхът лежи на Ox. При комплексни корени пресичане с Ox няма.

Методи за решаване

  1. Разлагане на множители — удобно при „приятни“ коефициенти и малко c.

  2. Квадратна формула — универсален метод чрез дискриминанта.

  3. Допълване до квадрат — когато лесно се образува (x + p)².

  4. Графичен поглед — за брой решения и интуиция.

Примери стъпка по стъпка

Пример 1: Разлагане на множители

Реши: x² − 5x + 6 = 0

Решение: Търсим две числа с произведение 6 и сума −5: −2 и −3. Следователно (x − 2)(x − 3) = 0, т.е.
x = 2 или x = 3.

Проверка: x₁ + x₂ = 5 = −b/a, x₁·x₂ = 6 = c/a.

Пример 2: Квадратна формула

Реши: 2x² + 3x − 2 = 0

Решение: D = 3² − 4·2·(−2) = 25, x = [−3 ± 5]/4. Значи x₁ = 1/2,
x₂ = −2.

Проверка: Сума = −3/2 = −b/a, произведение = −1 = c/a.

Пример 3: Графичен смисъл

За y = x² − 4x + 1 върхът е (2, −3), корените са x = 2 ± √3, параболата се
отваря нагоре.

Пример 4: Съвършен квадрат

x² + 4x + 4 = 0 дава (x + 2)² = 0 ⇒ x = −2 (двоен корен).

Пример 5: Общ множител

3x² − 12x + 9 = 0 ⇒ 3(x² − 4x + 3) = 0 ⇒ (x − 1)(x − 3) = 0 ⇒
x = 1 или x = 3.

Бързи проверки и Виет

  • x₁ + x₂ = −b/a, x₁·x₂ = c/a

  • Ако c = 0, тогава x(ax + b) = 0 и единият корен е 0

  • Ако a и c са с един и същ знак, корените не са с различни знаци

  • Симетрия: около x = −b/(2a)

Кратък тест

  1. x² − 9 = 0

  2. 3x² − 12x + 9 = 0

  3. Връх на y = −2x² + 8x − 3

▶ Отговори

  1. x = ±3

  2. D = 36, x = 3 или x = 1

  3. x_v = 2, y_v = 5, връх (2, 5)

Домашно упражнение (12 задачи)

  1. 4x² + 4x − 3 = 0

  2. x² − 2x − 8 = 0

  3. 5x² − 20x + 20 = 0

  4. (x − 1)(x − 7) = 0

  5. 2x² + x + 10 = 0

  6. x² + px + q = 0 за p = −5, q = 6

  7. Нормализирай и реши: −x² + 6x − 8 = 0

  8. Намери реалните корени и провери Виет

  9. Графично: връх за y = x² + 2x − 3

  10. Приложно: време на полет при y(t) = −5t² + 20t + 1 (кога y = 0?)

  11. Общо решение: ax² + bx = 0

  12. Разложи: x² − 7x + 12 = 0

Обобщение

  • Избирай метода според уравнението: разлагане, допълване, формула.

  • Проверявай с Виет и чрез замяна.

  • Ползвай графичен поглед за интуиция.

  • Практиката води до увереност.

Сподели в: