Лице на триъгълник: различни формули според данните

от Стефан Стратиев, 13/11/2025

Въведение

Лицето на триъгълник е една от най-често срещаните величини в училищната геометрия. В зависимост от това какви данни са дадени (страни, височини, ъгли), избираме най-подходящата формула. В тази статия ще:

• • преговорим трите основни подхода: по страна и височина, по две страни и включен ъгъл, по трите страни (Херон)
• • разгледаме типични ситуации и капани
• • решим примери стъпка по стъпка
• • проверим знанията с кратък тест
• • предложим домашни упражнения с нарастваща трудност

Целта е не само да запомниш формулите, а да разбереш кога коя е уместна и как да проверяваш резултата за разумност (единици, приблизителни оценки, сравнения).

Основни понятия

• Височина към страна a: перпендикулярът от срещуположния връх към правата, съдържаща страна a. Обозначаваме ha.

• Полупериметър: p = (a + b + c) / 2.

• Синус на ъгъл γ: отношение на височината към хипотенузата в подходящ триъгълник; числена стойност между 0 и 1 за γ в (0°, 180°).

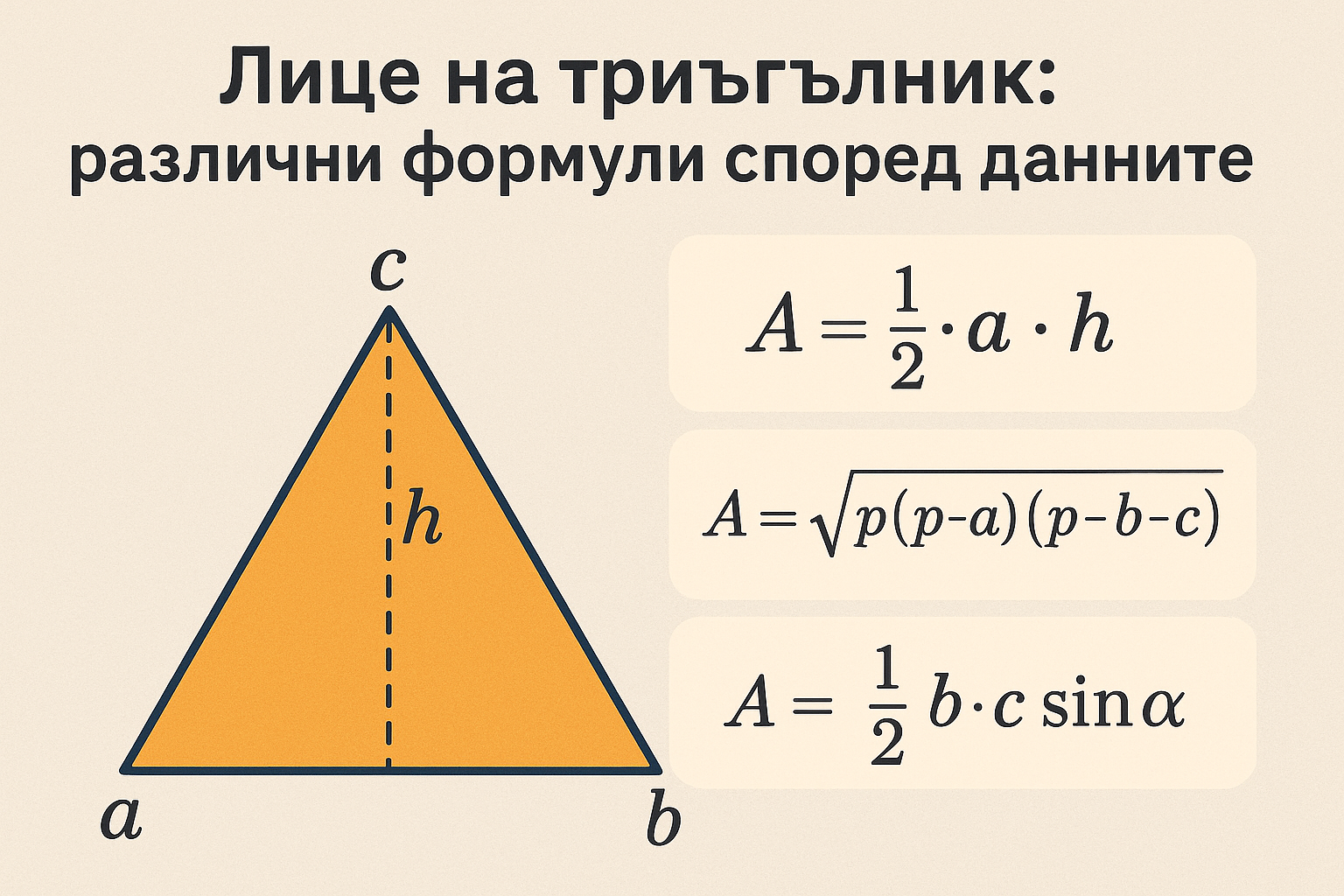
Основни формули за лице S:

1. По страна и височина към нея: S = a · ha / 2.

2. По две страни и включен ъгъл γ: S = a · b · sin(γ) / 2.

3. Формула на Херон (по трите страни): S = √( p(p − a)(p − b)(p − c) ).

Забележка: И в трите случая резултатът е в квадратни единици (cm2, m2 и т.н.).

Кога коя формула да използвам?

• Дадена е височина към конкретна страна → използвай S = a · ha / 2.

• Дадени са две страни и ъгълът между тях → използвай S = a · b · sin(γ) / 2.
  Важно: ъгълът трябва да е „включен“ между двете страни.

• Дадени са трите страни → използвай Херон.
  Преди това провери дали страните могат да образуват триъгълник: a < b + c, b < a + c, c < a + b.

Практичен съвет: Ако имаш правоъгълен триъгълник с катети x и y, то S = x · y / 2 (специален случай на 1)).

Примери стъпка по стъпка

1) По страна и височина

Дадено: a = 10 cm, ha = 6 cm. Намери S.

Решение:

• Използваме S = a · ha / 2.

• S = 10 · 6 / 2 = 60 / 2 = 30 cm2.

Проверка: Единиците са cm2. Числото е разумно спрямо a и ha.

2) По две страни и включен ъгъл

Дадено: a = 7 cm, b = 9 cm, γ = 30° (ъгълът между a и b). Намери S.

Решение:

• Използваме S = a · b · sin(γ) / 2.

• sin(30°) = 1/2.

• S = 7 · 9 · (1/2) / 2 = 63 · (1/2) / 2 = 31.5 / 2 = 15.75 cm2.

Забележка: Честа грешка е да се дели само веднъж. Формулата има „делено на 2“ след умножението с sin(γ).

3) По трите страни (Херон)

Дадено: a = 7 cm, b = 8 cm, c = 9 cm. Намери S.

Решение:

• Проверка за триъгълник: 7 < 8+9, 8 < 7+9, 9 < 7+8 → вярно.

• Полупериметър: p = (7+8+9)/2 = 24/2 = 12.

• S = √( p(p − a)(p − b)(p − c) ) = √( 12 · (12−7) · (12−8) · (12−9) ) = √( 12 · 5 · 4 · 3 ).

• 12 · 5 · 4 · 3 = (12 · 4) · (5 · 3) = 48 · 15 = 720.

• S = √720 = √(144 · 5) = 12√5 ≈ 26.83 cm2.

Проверка: Приблизително 27 cm2 изглежда разумно за страни около 7–9 cm.

4) Специален случай: правоъгълен триъгълник

Дадено: катети x = 6 cm и y = 8 cm. Намери S.

• S = x · y / 2 = 6 · 8 / 2 = 48 / 2 = 24 cm2.

Сравнение: Ако използваме и формула 2) по хипотенуза и катет с γ = 90°, sin(90°) = 1, пак получаваме S = (a · b) / 2, където a и b са катети.

Чести грешки

• Смесване на височини: ha е височина към страна a. Ако е дадена височина към друга страна, не я замествай безпринципно.

• Невключен ъгъл: При S = a · b · sin(γ) / 2, γ трябва да е ъгълът между страните a и b. Ако γ е друг ъгъл, резултатът ще е грешен.

• Грешки при Херон: неправилно изчисляване на p или на произведението p(p − a)(p − b)(p − c). Работи внимателно, групирай множителите удобно.

• Единици: Забравени квадратни единици в отговора.

• Нереалистични резултати: Ако S излезе твърде голям/малък спрямо дадените дължини, прегледай смятанията.

• ---

  Кратък тест (с решения)

  1. a = 12 cm, ha = 5 cm → S = ?

  2. a = 9 cm, b = 14 cm, γ = 60° → S = ?

  3. a = 5 cm, b = 5 cm, c = 6 cm → S = ? (Херон)

  4. Правоъгълен триъгълник с катети 7 cm и 3 cm → S = ?

  Решения:

  1. S = a · ha / 2 = 12 · 5 / 2 = 60 / 2 = 30 cm2.

  2. sin(60°) = √3/2. S = 9 · 14 · (√3/2) / 2 = 126 · (√3/2) / 2 = 63 · √3 / 2 ≈ 54.56 cm2.

  3. p = (5+5+6)/2 = 8. S = √(8 · (8−5) · (8−5) · (8−6)) = √(8 · 3 · 3 · 2) = √(144) = 12 cm2.

  4. S = 7 · 3 / 2 = 21 / 2 = 10.5 cm2.

  ---

  Домашно упражнение

  Реши и запиши кратки проверки за разумност.

  1. a = 15 cm, ha = 8 cm.

  2. a = 11 cm, b = 13 cm, γ = 45°.

  3. a = 9 cm, b = 10 cm, c = 5 cm.

  4. Равнобедрен триъгълник с бедра 10 cm и основа 12 cm.

  5. Правоъгълен триъгълник с хипотенуза 13 cm и катет 5 cm. Намери лицето.

  6. a = 6.4 cm, ha = 4.9 cm.

  7. a = 8 cm, b = 9 cm, γ = 120°.

  8. a = 7.5 cm, b = 7.5 cm, c = 7.5 cm.

  9. Катети 2.4 cm и 3.1 cm.

  10. Страни 4 cm, 9 cm, 14 cm. Възможен ли е триъгълник?

  Подсказки:

  • Задача 4: Можеш да приложиш Херон. Проверка: p = (10+10+12)/2.

  • Задача 5: Първо намери другия катет по Питагор, после S = катет · катет / 2.

  • Задача 7: За тъпи ъгли sin(120°) = sin(60°) = √3/2.

  • Задача 10: Провери неравенствата за триъгълник.

  • ---

    Обобщение

    • Избирай формулата според наличните данни.

    • Проверявай дали ъгълът е включен при S = a · b · sin(γ) / 2.

    • При три страни използвай Херон, но първо провери възможността на триъгълник.

    • Винаги посочвай квадратни единици и прави бърза проверка за разумност.